Last week in this space, we discussed the ritual of Rachel Homan’s opponents throwing their first shot in the rings when they didn’t have hammer in the first end. This puts the end on the road to the transactional blank, where both teams play a series of routine hits to produce a score of zero. It’s the worst part of competitive curling for the viewer and should probably be outlawed. It’s the equivalent of starting a basketball game with five minutes of passing drills or a football game with seven minutes of kneel-downs.
But I guess there’s no easy way to prohibit it and far be it for me in my sixth blog post to suggest major rules changes to a centuries-old sport. It would be best for everyone if the approach just disappeared due to natural causes. We saw that when playing top teams, blanking the first end gives the team with last rock a slight boost in win probability, so it would seem that cooperating in a blank is counterproductive for the non-hammer team.
But this strategy – if one can call it that – is still employed a lot and when it is, there are two common reasons given for the non-hammer team’s approach by the Russ Howards and Cheryl Bernards of the world.
While these seem like good reasons, I’m skeptical of both. In terms of figuring out the ice, both teams have an equal opportunity to do that, so we need a good reason why one team will get more benefit than its opponent. And the second point faces a similar challenge. Does saving time on the clock benefit you more than your opponent? If so, maybe work on your ability to manage the clock.
The real problem is that history indicates that blanking the first end helps the hammer team slightly. And the two variables mentioned are baked in to the historical analysis. So you have to convince yourself that you’ll benefit from either of those two factors by more than the 2-to-3 percent that the blank is typically worth to the hammer team, and in a way that past teams using the strategy didn’t benefit.
With respect to playing Rachel Homan specifically, there’s a theory in poker that if you sit down at the table and can’t figure out who the fish is, it’s probably you. As mentioned last week, no team in the world blanks the first end with hammer more often than Homan. So if you are willing to play along with a strategy that Homan clearly prefers, you should ask yourself why you’re so sure it will put her at a disadvantage.
That said, there’s another reason the non-hammer team might find the blank appealing, especially as an underdog. As commenter Chris noted in the last piece, there’s a theory that you’re shortening the game. In timed sports like basketball and football, strategies to run the clock ensure there will be fewer chances for the favorite to show its superior skill.
But what shortening the game is really about in those sports is increasing variance and I think the path to doing that is a little more complicated in curling. Clearly, you’d rather play 10 ends against Homan than 16, but based on history, shortening the game only has benefits for the team with hammer. This is a topic that deserves its own post at some point.
There is one possible legitimate reason I can think of to throw the first shot in the rings, however. While I call it the “transactional” blank (as distinguished from the strategic blank, which often involves some skilled shot-making), it’s not merely a transaction, even for the best teams. Mistakes are often made, and if the hammer team makes mistakes often enough, then throwing into the rings on the first shot can be the right approach in the long run.
Given our win probability analysis, the hammer team gains 2.4% from a blank and loses 4.5% from a force in the first end. If both teams execute their hits up to the final shot and our opponent hits and sticks on their last rock more than 35% of the time, the non-hammer team gains some win probability over the long term. In fact, the threshold could be lower than that since blank and force aren’t the only two possibilities. Our opponent could also flash, producing a steal giving us a 15% boost in win probability.
Now the observant reader might say, ‘a player like Homan never flashes in that situation’. Well, I’ve got news for you.
To be fair, Homan’s playing a hit-and-stick there and thus less weight than if she wanted to hit and roll out. In true hit-and-roll situations, she was successful on 16 of 19 attempts (84%) by my count, with all three misses resulting in forces after the shooter stayed in the rings. Far from perfect, but seemingly enough to deter the transactional blank approach based on our back-of-the-envelope math.
It’s true Rachel probably never flashes when trying to get the blank, but it’s also true you can put together a decent-length video of her team making mistakes in the first end. And the reason I know this is that I have watched every one of Homan’s first ends with hammer that is available on YouTube since 2015. (These may not be all of them, so if you find others let me know and I’ll update the list. I’m excluding Continental Cup games since they are not eligible for points in the order of merit and feel like games where little is at stake.)
Here are those ends along with whether the opponent’s first shot went into the rings and the eventual score for the end.
Yr Event Round Opponent In Rings? Score 20 Scotties 3/4 McCarville Yes 0 20 Scotties Pool McCarville Yes +2 20 Ontario Scotties Finals Duncan Yes -1 20 Ontario Scotties Pool Murphy Yes* 0 20 Ontario Scotties Pool Froud Yes +2 19 Canada Cup Finals Fleury No +1 19 Scotties Pool Jones Yes* 0 18 Canada Cup Pool Flaxey Yes 0 18 World Cup Suzhou Final Hasselborg Yes* 0 17 Worlds Final Sidorova Yes 0 17 Worlds 1/2 Sidorova Yes 0 17 Worlds Pool Sidorova Yes +3 17 Worlds Pool Muirhead Yes 0 17 Worlds Pool Gaspari Yes 0 17 Scotties SF McCarville Yes 0 17 Scotties SF McCarville Yes 0 17 Scotties Pool Bélisle Yes 0 17 Scotties Pool Carey No +1 17 Ontario Scotties Pool Auld Yes +1 17 Roar of the Rings Pool Sweeting Yes +1 17 Roar of the Rings Pool Tippin Yes +2 17 Roar of the Rings Pool McCarville Yes 0 17 Roar of the Rings SF Jones Yes 0 16 CanadInns Classic Pool Sigfridsson No +2 16 Canada Cup SF Einarson No +1 16 Canada Cup Pool Carey Yes 0 15 Canada Cup Final Sweeting Yes 0 15 Canada Cup Pool Sweeting No +4 15 Prairie Showdown Pool Scheidegger No +2 15 Scotties Pool Sweeting No -1 15 Scotties Pool Lawton Yes 0 *Call was guard but shot ended up in the rings
That’s 31 ends of curling and in 24 of them the opponent offered the blank with their first shot (though at least three times it was by accident). That gives us a chance to see the distribution of outcomes when a Homan opponent puts the first rock in (and when it doesn’t). Here’s the summary:
First rock Score Rings Guard WPA(%) -1 1 1 -14.9 0 17 0 +2.4 +1 1 3 -4.5 +2 4 2 +14.9 +3 1 0 +22.0 +4 0 1 +34.0
WPA is the win probability added for each score based on our analysis of games between top 15 teams from the previous post. So each steal of one in the first end decreases the hammer’s win probability by 14.9%. Each blank improves the hammer’s win probability by 2.4%, etc. You can read the rest. Please note the values for +3 and +4 are estimates due to their rarity.
If we average the results for each choice, we don’t see a definitive difference in the strategies. When the opponent throws in, Homan gains an average of 4.3% per end, and when a guard is thrown, Homan gains 5.1%. With just seven cases of the latter, we don’t have nearly enough data to draw any conclusions, especially given the win probability estimates for each score are based on limited data themselves. Homan’s score of four against Sweeting in the 2015 Canada Cup is really doing some heavy lifting for that approach.
Look at it another way: In just two of the 24 ends with the first stone in the rings was there a force/steal, while four of the seven guards produced a force/steal. And if Homan just makes the hit-and-stick against Duncan and gets her deuce instead of giving up one, she would have averaged a 5.5% gain on the cases where the first rock went in. When one shot can make that big of a difference we need more data. It’s safe to say we have a ways to go before we can back the overwhelming preference of Homan’s opponents.
While I come away from this exercise still wishing the first-end blank would go away, I have a greater appreciation for the transactional blank process after watching a bunch of first ends play out. In 26% of the cases where the opponent threw in against Homan, there actually wasn’t a blank. And surely that percentage increases as skill level decreases. (This is why the transactional blank isn’t a thing in beginner’s league.) But the mistakes benefited Homan five out of seven times. If you’re going to try to blank Homan, you best not miss.
An interesting background influence on this approach is that women in general prefer to blank the first end more than men, despite men generating significantly more blanks from the third end on.
This chart only includes data for games scheduled for 10 ends…
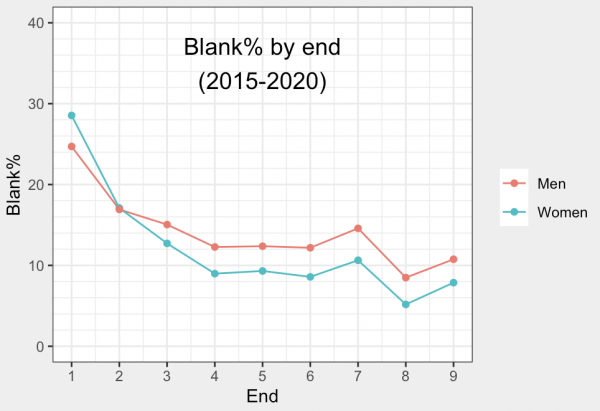
After all of this, we’re back where we started. The non-hammer team likes to blank the first end against Homan an awful lot considering there’s flimsy evidence indicating it’s obviously the optimal approach. Remarkably, opponents think Homan is the fish in the first end. History doesn’t provide a conclusive verdict on that view, and unless more of Homan’s opponents have the guts throw a guard with their first shot, we may never know for sure.
Update! Thanks to commenter Johan for pointing out the shot descriptions for the Grand Slam events at CurlingZone. That provides us with a lot more data. The additional games are listed at the end, but here’s the summary now including the slams.
First rock
Score Rings Guard WPA(%)
-2 1 2 -25.0
-1 1 6 -14.9
0 35 7 +2.4
+1 7 8 -4.5
+2 8 7 +14.9
+3 2 1 +22.0
+4 0 1 +34.0
The tally on win probability is that Homan gains 3.3% on average when the first rock is in the rings and just 0.5% when it’s a guard. It’s still close, but there are enough cases now (54 in the rings and 32 guards) where it’s safe to say that throwing in the rings is not clearly the best strategy. It’s also interesting that the difference between a guard and a shot in the rings is almost the same as the value of a first-end blank with hammer.
Here are the additional individual cases:
Yr Event Round Opponent In Rings? Score
16 Masters Pool Paetz No +1
16 Masters Pool Rocque No +3
16 Masters Pool Muirhead No +3
16 Masters Pool Jones No -1
16 Masters Pool Flaxey No -1
16 Tour Challenge Pool Ogasawara Yes 0
16 Tour Challenge Pool Fleury Yes +1
16 Tour Challenge QF Englot Yes +2
16 National Pool Carey Yes +3
16 National Pool McCarville Yes +1
16 National Pool Flaxey No +2
16 National Pool Fleury No +2
17 Canadian Open Pool Harrison No -2
17 Canadian Open Pool Sidorova No 0
17 Canadian Open TB Harrison No +1
17 Players Pool Wang Yes +1
17 Players QF Sweeting Yes 0
17 Champions Cup Pool Schiedegger Yes 0
17 Champions Cup Pool Sweeting Yes +1
17 Champions Cup Pool Einarson No -1
17 Champions Cup QF Jones Yes 0
17 Tour Challenge Pool Harrison No +1
17 Tour Challenge Pool Wang Yes +1
17 Tour Challenge Pool Muirhead No +1
17 Masters Pool Englot Yes -2
17 National Pool Harrison No +2
17 National Pool Einarson Yes +2
17 National Pool Englot Yes 0
18 Players Pool Roth Yes 0
18 Champions Cup Pool Feltscher Yes 0
18 Champions Cup Pool Paetz No -2
18 Masters Pool Fleury Yes 0
18 Masters Pool Einarson Yes +1
18 Masters Pool K Jones Yes 0
18 Masters QF Robertson No -1
18 Masters SF Carey No +2
18 Masters Final Hasselborg No +1
18 Tour Challenge Pool Sinclair Yes 0
18 Tour Challenge Pool Christensen Yes 0
18 Tour Challenge Pool Carey Yes 0
18 Tour Challenge QF Walker Yes 0
18 Tour Challenge SF Roth No 0
18 National Pool Harrison No 0
18 National Pool Muirhead Yes 0
18 National Pool Einarson No -1
18 National QF Harrison Yes 0
18 National SF Jones No 0
18 National Final Einarson No 0
19 Players Pool Silvernagle Yes 0
19 Players Pool Stern Yes +2
19 Players TB Fujisawa No 0
19 Masters Pool Yoshimura Yes +2
19 Masters Pool Stern Yes 0
19 National Pool Yoshimura Yes 0
19 National Pool Silvernagle No 0